Topics / リスク（標準偏差）とは

リスク（標準偏差）とは

まず大前提として、過去のリターン実績を集計していくと、平均値（期待リターン）を中心とした山の形になると考えられます。これを「正規分布曲線」と呼んでいます。データが少ないと「そんなことない」というケースもありますが、データが多ければ多いほどこの釣鐘状の形に近づいていきます。

たとえば「大数の法則」というものがあります。（ここはリスクの説明とは切り離して、正規分布になることの補足説明と考えてください。）サイコロを振って1の目の出る確率は、振る回数を増やせば増やすほど6分の1に近づいていきます。数を増やせば、発生する確率が一定値に近づくということで、これを大数の法則といいます。個々人にとっては偶発的な事故であっても、大量のデータで見ることによってその発生率を全体として予測できるということになり、この統計的確率は損害保険や生命保険に生かされています。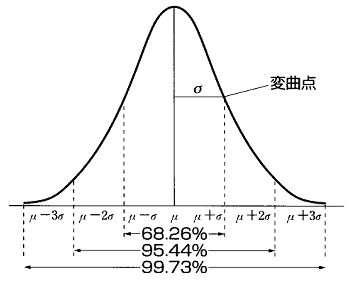

正規分布

データ数が多ければ多いほど、釣鐘状の形になると理解していただき、話を次に進めましょう。リスクは統計学で使う「標準偏差」で表されます。つまり平均値（山の頂上の位置）から、どれだけ離れているかを計算します。平均値を「μ（ミュー）」、標準偏差は「σ（シグマ）」という記号を使います。（日本地図上の

温泉マークみたいなものです。ゴッチャにならないよう記号化しているだけですが、ギリシャ文字なのでシックリくるまで逆に混乱しちゃいますね。）

上の図を見ていただくと、「平均値±σ」が６８．２６％となっています。つまり統計上、平均値から±１標準偏差《１σ》の範囲内に約３分の２の確率で入ることを表します。また「平均値±２σ」（標準偏差を２倍したもの《２σ》をプラスマイナスする）が９５．４４％、「平均値±３σ」（標準偏差を３倍したもの《３σ》をプラスマイナスする）なら９９．７３％の確率で入りますよということです。ですからリスクというのは、あくまで過去、「平均値から３分の２の確率で入った範囲」を「バラツキ具合」として示しているものだとお考え下さい。

具体的な計算例をご紹介しましょう。

５０人生徒がいる、あるクラスのテストの平均点が５５点でした。（得点の合計は２，７５０点、５０人で割ると５５点でしたということです。）ではこのクラスの成績分布はどうなっていたでしょうか？（５０人はデータとして少ないかもしれませんが、正規分布する前提です。）平均値５５点（μ）からのバラツキ具合（σ）を実際に計算していきましょう。これがリスクの計算方法です。

１人目Ａ君の成績は６０点、平均値５５点からの差異は５点です。
２人目Ｂ君の成績は５０点、平均値５５点からの差異は－５点です。

今二人だけ平均値からの差異（バラツキ具合）を計算しましたが、この二人だけの差異を合計すると「５－５＝０」となってしまい、平均値からのバラツキ具合が計測できなくなってしまいます。プラスとマイナスが混在するとこうした事態が発生することから、やり方を変えることにします。まずはマイナスの差異が発生しないように、差異を２乗してやります。そして差異の合計を計算し、その平均を算出したあとで、２乗を√を使って解くことにします。

１人目Ａ君の成績は６０点、平均値からの差異は５点です。２乗すると２５になります。
２人目Ｂ君の成績は５０点、平均値からの差異は－５点です。２乗すると２５になります。
３人目Ｃ君の成績は５８点、平均値からの差異は３点です。２乗すると９になります。
………

こうして５０人各々を計算した結果、２乗した差異の合計が４，２００になったとします。
平均の差異は４，２００÷５０人で８４と計算されますので、これを√を使って２乗を解きますと、９．１６という差異が計算されました。この９．１６がこのクラスのテスト結果におけるリスク（バラツキ具合、ブレ幅）になります。リスクの数値、つまり標準偏差が小さければ、それだけブレ幅が小さいわけで、ということはリスクが低いことになりますし、逆に標準偏差が大きければ、それだけリスクが高いことになります。

こうして算出されたリスクの数値から見えてくる、このクラスのテスト成績の分布は、５５点±９．１６の範囲内【４５．８４点～６４．１６点】に３分の２の生徒が入ったことになります。※この範囲外に３分の１の生徒がいることを忘れないこと。
５５点±（９．１６×２）の範囲【３６．６８点～７３，３２点】に約９５％、
５５点±（９．１６×３）の範囲【２７．５２点～８２．４８点】に約９９％
が入ったことになります。